Developer's Guide--Part IV
recognition
MFCC:
The human hearing system is a special nonlinear system. The sensitiveness it response to different signals is different, primarily a logarithm. In recent years, a parameter called Mel-scaled Cepstrum Coefficients, which can make use of the specialty of human ears effectively, has been applied widely, In short, MFCC. Mass researches indicate that MFCC parameter can improve the discriminating ability of the system more efficiently.
MFCC parameter is calculated using ＾bark￣ as its frequency unit. The translation formula of bark and the linear frequency is:
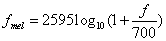
MFCC parameter is calculated according to frames. First we get the power spectrum S(n) of the signal frame using FFT and translate it into power spectrum of the MEL frequency. This need to set several band-pass filters in the area of vocal frequency spectrum.
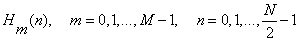
M is the number of filters, normally set to 24. N is the number of vocal signal points. Always set to 256 for calculating convenience. The frequency area of filters is a simple triangle with a center frequency 
. They distribute uniformity in the MEL frequency axis, while the distance between changes in proportion with m in the linear frequency axis. And there is a linear area between 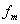and f in the low-frequency area. The parameters of the band-pass filter are figured out before calculating the MFCC parameters.
MFCC parameters are always calculated through the following processes:
• First determine the number of sampling points in every frame's vocal sampling sequence, Our system set N=256 points. Set pre-emphasize and then DFFT to each frame of s(n) to get s'(n). Mod s'(n)and square the result, then we obtained the discrete power spectrum s(n).
• Calculate the products of s(n) and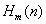 
in every discrete frequency point and add them together. Then we obtain M parameters of 
.
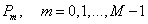• Calculate the natural logarithm of 
as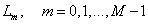 
.
• Calculate the discrete cosine transition of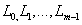 
,we have the result 
.
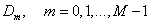• Abandon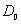 
representing the direct current part. Use 
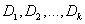as MFCC parameters. where K=12.
DTW:
Speech is a time-dependent process. Several utterances of the same word are likely to have different durations, and utterances of the same word with the same duration will differ in the middle, due to different parts of the words being spoken at different rates. To obtain a global distance between two speech patterns (represented as a sequence of vectors) a time alignment must be performed.
This problem is illustrated in Fig.4.1, in which a ＾time-time￣ matrix is used to visualize the alignment. As with all the time alignment examples the reference pattern (template) goes up the side and the input pattern goes along the bottom. In this illustration the input ＾SsPEEhH￣ is a ｀noisy' version of the template ＾SPEECH￣. The idea is that ｀h' is a closer match to ｀H' compared with anything else in the template. The input ＾SsPEEhH￣ will be matched against all templates in the system's repository. The best matching template is the one for which there is the lowest distance path aligning the input pattern to the template. A simple global distance score for a path is simply the sum of local distances that go to make up the path
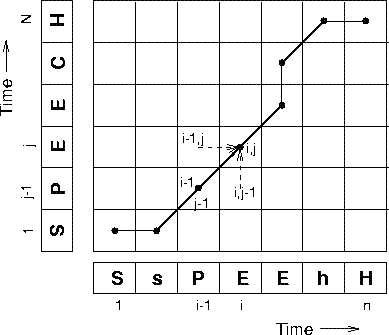
Fig.4.1. Illustration of a time alignment path between a template pattern ＾SPEECH￣ and a noisy input ＾SsPEEhH￣
In order to find the best-matching (= lowest global distance) path between an input and a template,we could evaluate all possible paths - but this is extremely inefficient as the number of possible paths is exponential in the length of the input. Instead, we will consider what constraints there are on the matching process (or that we can impose on that process) and use those constraints to come up with an efficient algorithm. The constraints we shall impose are straightforward and not very restrictive:
• Matching paths cannot go backwards in time;
• Every frame in the input must be used in a matching path;
• Local distance scores are combined by adding to give a global distance.
For now we will say that every frame in the template and the input must be used in a matching path. This means that if we take a point (i,j) in the time-time matrix (where i indexes the input pattern frame, j the template frame), then previous point must have been (i-1,j-1), (i-1,j) or (i,j-1) . The key idea in dynamic programming is that at point (i,j) we just continue with the lowest distance path from (i-1,j-1), (i-1,j) or (i,j-1).
This algorithm is known as Dynamic Time Warping (DTW). DP is guaranteed to find the lowest distance path through the matrix, while minimizing the amount of computation. The DP algorithm operates in a time-synchronous manner: each column
of the time-time matrix is considered in succession (equivalent to processing the input frame-by-frame) so that, for a template of length N, the maximum number of paths being considered at any time is N.
If D(i,j) is the global distance up to (i,j) and the local distance at (i,j) is given by:
D(i,j)=min[D(i-1,j-1), D(i-1,j), D(i,j-1)]+d(i,j)
Given that D(1,1) = d(1,1) (this is the initial condition), we have the basis for an efficient recursive algorithm for computing D(i,j). The final global distance D(n,N) gives us the overall matching score of the template with the input. The input word is then recognized as the word corresponding to the template with the lowest matching score. (Note that N will be different for each template.)
For basic speech recognition DP has a small memory requirement, the only storage required by the search (as distinct from the templates) is an array that holds a single column of the time-time matrix.
The pseudocode for this process is:
calculate first column (predCol)
for i=1 to number of input feature vectors
curCol[0]=local cost at (i,0) + bal cost at (i-1,0)
for j=1 to number of template feature vectors
curCol[j]=local cost at (i,j) + minimum of global costs at (i-1,j), (i-1,j-1) or (i,j-1)
end
predCol=curCol
end
minimum global cost is value in curCol[number of template feature vectors]
In order to effect a recogniser, the input pattern is taken and the above process is repeated for each template file. The template file which gives the lowest global cost is the word estimate.
back to top
