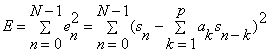Developer's Guide--Part II
Time Analysis
Frequency Analysis
Cepstral Analysis
WRLS-VFF Analysis
Time Analysis
For time domain analysis, we assume that all data are windowed. A frame is a windowed segment of data. In speech research, we use short-time analysis of data, that is, the data are windowed. Thus, we use an analysis data frame. Data frames can be ovelapped or not. The result of the frame analysis of data is usually a number, or perhaps a small set of numbers, that is less than the number of data samples within the data window. This set of numbers varies with time, that is, it forms a waveform. So we analyze data to reduce the number of data samples in a given data waveform to a small set of values or features. These features can be used to determine characteristics of speech.
Energy and ZCR:
One of the most common short-time analysis methods is the short-time average energy of a signal. If 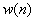 is the data window for is the data window for 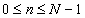 and is zero otherwise, and and is zero otherwise, and 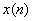 is the data record, then the short-time average energy is is the data record, then the short-time average energy is
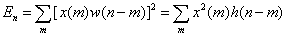
where 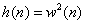 . Thus, . Thus, 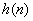 is a window (filter) that affects the short-time energy function. If this window is very short, then its bandwidth is large and there is little filtering of the data by the window. If the window is very long, then the window bandwidth is narrow, and there is a great deal of filtering of the data. We select the window parameters (or type of window) to provide “good” data smoothing. The type of window selected can depend on the application or task but for speech, the window used is usually the hamming window. is a window (filter) that affects the short-time energy function. If this window is very short, then its bandwidth is large and there is little filtering of the data by the window. If the window is very long, then the window bandwidth is narrow, and there is a great deal of filtering of the data. We select the window parameters (or type of window) to provide “good” data smoothing. The type of window selected can depend on the application or task but for speech, the window used is usually the hamming window.
The short-time average zero-crossing rate is used to estimate the frequency of voicing. Suppose we are given a sampled sineware of frequency  that is sampled at rate that is sampled at rate 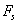 . The number of samples in a period is . The number of samples in a period is 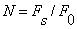 . For a periodic signal, we have two zero-crossings per period, which is . For a periodic signal, we have two zero-crossings per period, which is 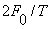 , where , where 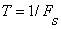 . To estimate . To estimate 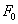 , count the number of zero-crossings in the sampled data over some time interval, , count the number of zero-crossings in the sampled data over some time interval, 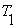 . Then . Then 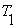 is the number of samples in is the number of samples in 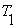 divided by divided by 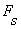 , that is , that is 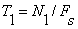 or or 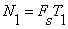 . The average number of zero-crossings per sample is . The average number of zero-crossings per sample is 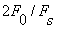 , thus , thus 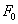 =(average number of zero-crossings)/(2 =(average number of zero-crossings)/(2 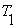 ). So the zero-crossing rate algorithm is the following: ). So the zero-crossing rate algorithm is the following:
• Count the number of samples in the data between sign changes. This interval (number of samples) represents 1/2 the period or 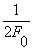 . .
• The average number of samples between sign changes is 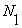 . .
• 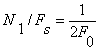
• 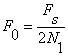
The short-time energy and zero-crossing functions are useful for estimating word and phoneme boundaries.
Autocorrelation:
Various applications call for autocorrelation estimates, including data modeling such as linear prediction and power spectral estimation.
The biased autocorrelation estimate, is expressed as
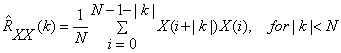
where 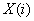 is a zero mean Gaussian random sequence. Although this estimate is biased, It is asymptotically unbiased as N increases for k fixed. And the variance is approximately is a zero mean Gaussian random sequence. Although this estimate is biased, It is asymptotically unbiased as N increases for k fixed. And the variance is approximately
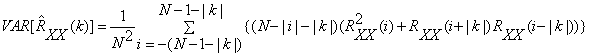 This estimate is also consistent as N increases, provided k is fixed. It can also be shown that this estimate does have its largest value at the origin, which in correlation matrix terms means that this estimate is positive definite. This estimate is also consistent as N increases, provided k is fixed. It can also be shown that this estimate does have its largest value at the origin, which in correlation matrix terms means that this estimate is positive definite.
back to top
Frequency Analysis
In this part we mainly discuss the Linear Prediction(LP) Analysis and estimates of the power spectrum.
Linear prediction analysis of speech is historically one of the most important speech analysis techniques. The basis is the source-filter model where the filter is constrained to be an all-pole linear filter. This amounts to performing a linear prediction of the next sample as a weighted sum of past samples: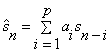 . .
Given N samples of speech, we would like to compute estimates to 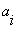 that result in the best fit. One reasonable way to define “best fit” is in terms of mean squared error. These can also be regarded as “most probable” parameters if it is assumed the distribution of errors is Gaussian and a priori there were no restrictions on the values of that result in the best fit. One reasonable way to define “best fit” is in terms of mean squared error. These can also be regarded as “most probable” parameters if it is assumed the distribution of errors is Gaussian and a priori there were no restrictions on the values of 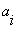 . .
The error at any time, 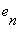 , is: , is:
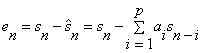
Hence the summed squared error, E , over a finite window of length N is:
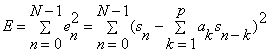
The minimum of E occurs when the derivative is zero with respect to each of the
parameters, 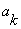 . As can be seen from equation (3.2.1) the value of E is quadratic in
each of the 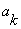 therefore there is a single solution. Very large positive or negative values of 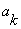 must lead to poor prediction and hence the solution to 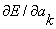 =0 must be a minimum. Hence differentiating equation(3.2.1) with respect to 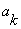 and settingzero gives the set of p equations:
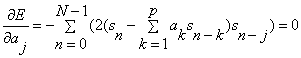 (3.2.1) (3.2.1)
then we can get :
rearranging the equation gives
Define the covariance matrix, r with elements :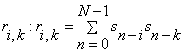 . Now we can write the following equation as: . Now we can write the following equation as: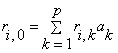 or in matrix form: or in matrix form:
or simply 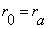 . .
Hence the Covariance method solution is obtained by matrix inverse: 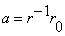 . .
Note that:
• This method can be used on much smaller sample sequences (as end discontinuities are less of a problem)
• There is no need to window the data while calculating and it has high precision
• There is no guarantee of stability (but you can check for instability)
Burg method:
Another linear prediction method is called Burg method. In contrast to the Covariance method, w hich estimate the LP parameters directly, the Burg method estimates the reflection coefficients first, and then uses the Levinson recursion to obtain the LP parameter estimates. The reflection coefficient estimates are obtained by minimizing estimates of the prediction error power for different order predictors in a recursive manner.

make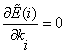 , then we have: , then we have:
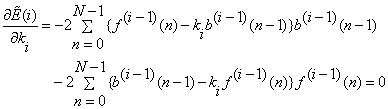
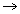
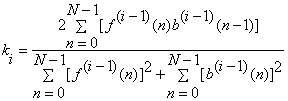
RMEL method:
The technique is a closer approximation to the true maximum likelihood estimator than that obtained using linear prediction techniques. The advantage of the new algorithm is mainly for short data records and/or sharply peaked spectra. Simulation results indicate that the parameter bias as well as the variance is reduced over the Yule-Walker and the forward-backward approaches of linear prediction. Also, spectral estimates exhibit more resolution and less spurious
peaks. A stable all-pole filter estimate is guaranteed. The algorithm operates in a recursive model order fashion, which allows one to successively fit higher order models to the data.
PLP method:
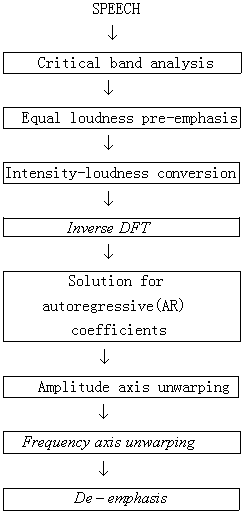
The perceptual linear prediction(PLP) analysis technique is based on well established psychophysical concepts of hearing. The speech signal is filterd by a critical band filter bank followed by an equal loudness pre-emphasis, and an intensity to loudness adjustment using the intensity-loudness power law. The auditory spectrum is then modeled by an LP model. The PLP analysis yield an auditory spectrum is nonuniform. In the higher frequency range it has less resolution, which agrees with the characteristics of the human auditory system. The PLP method is more consistent with human hearing than the conventional LP method. The PLP method is computationally efficient and yields a low dimensional representation of speech. The block diagram of PLP analysis is show as follows:
Spectral estimation:
Many problems in electrical engineering require a knowledge of the distribution of the power of a random process in the frequency domain, for example, the design of filters to remove noise, to cancel signal echoes, or to represent features of a signal for pattern recognition.
The periodogram is defined as:
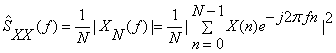
where X(n) is a random process.
back to top
Cepstral Analysis
Within human speech, there are two methods employed to form our words. These sounds are categorized into the voiced and unvoiced . For the voiced part, our throat acts like a transfer function. The vowel sounds are included in this category. The unvoiced part describes the "noisy" sounds of speech. These are the sounds made with our mouth and tongue (as opposed to our throat), such as the “f” sound, the “s” sound, and the "th" sound. This way of looking at speech as two seperable parts is known as the Source Filter Model of Speech or the Linear Separable Equivalent Circuit Model.
We define the complex cepstrum of data sequence as the inverse z-transform of the complex logarithm of the z-transform of the data sequence:
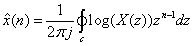
where 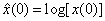 and X(z) is the z-transform of the data sequence x(n). Frequently, and X(z) is the z-transform of the data sequence x(n). Frequently, 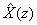 is used to denote the log[X(z)]. Then is used to denote the log[X(z)]. Then 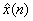 , the complex cepstrum, is the inverse z-transform of , the complex cepstrum, is the inverse z-transform of 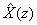 . The contour integration lies an annular region in which . The contour integration lies an annular region in which 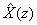 has been defined as singular valued and analytic. If we have the convolution of two sequences, then : has been defined as singular valued and analytic. If we have the convolution of two sequences, then : 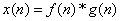 or or 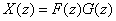 and and
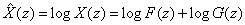 or or 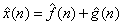 . Further, if . Further, if 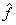 and and 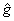 occupy different quefrency ranges, then the complex cepstrum can be liftered(filtered) to remove one or the other of the convolved sequences. Since the phase information is retained, the complex cepstrum is invertible. Thus, if occupy different quefrency ranges, then the complex cepstrum can be liftered(filtered) to remove one or the other of the convolved sequences. Since the phase information is retained, the complex cepstrum is invertible. Thus, if 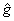 is rejected from is rejected from 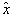 by liftering, then by liftering, then 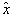 = =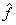 and we can then z-transform, exponentiate, and inverse z-transform to obtain the sequence f, that is, f and g have been deconvolved. An overall wavelet recovery or deconvolution(filtering) system is illustrated in Fig.3.1.1. and we can then z-transform, exponentiate, and inverse z-transform to obtain the sequence f, that is, f and g have been deconvolved. An overall wavelet recovery or deconvolution(filtering) system is illustrated in Fig.3.1.1.
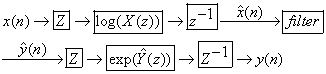
Fig.3.1.1. Calculating the complex cepstrum
back to top
WRLS-VFF Analysis
As an instruction in summary,I want ot show you that wrls-vff is adaptive weighted recursive least squares algorithm with a variable forgetting factor for short.
It aims to adjust the size of the data segment to be analyzed according to its time-varying characteristics,as during the during the transitions between vowels and consonants.
This algorithm can accurately estimate the vocal tract formants,anti-formants,and their bandwidths,be used for glottal inverse flitering,perform voiced (V)/unvoiced(U)/silent(S) classification of speech segments,estimate the input excitation(either white noise or periodic pulse trains),and estimate the instant of glottal closure.
After the instruction in concise,we will see entire description of this algorithm with input estimation in a stable version.First of all,we need to assume that the speech signal is generated by an autoregressive,moving average(ARMA) model,as the following equation:
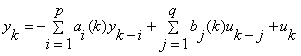
where yk denotes the kth sample of the speech signal,uk is the input excitation,(p,q) are the order of the poles and zeros,respectively,and ai(k) and bj(k) are the time-varying AR and MA parameters,respectively.
The next,we need to define a parameter vector θk and a data vector φk, by the following equations: 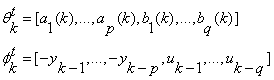
With these two assumptions,we can easily define our whole wrls-vff algorithm with input estimation as follow:
Prediction error: 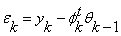
Gain update:
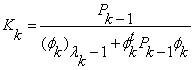
Forgetting factor:
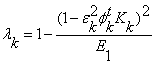
Input estimate:
a)Pulse input
if λk<λ0 then
 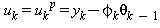
b)White noise input
if λk>λ0 then
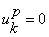 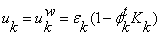
Parameter update:
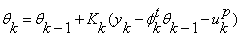
Covariance matrix:
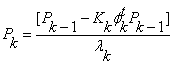
back to top
|