Developer's Guide--Part II

时域分析

频域分析

倒谱分析

WRLS-VFF分析

 

时域分析

　语音信号的时域分析就是分析和提取语音信号的时域参数。进行语音分析时，最先接触到并且也是最直观的是它的时域波形。语音信号本身就是时域信号，因而时域分析是最早使用，也是应用最广泛的一种分析方法，这种方法直接利用语音信号的时域波形。时域分析通常用与最基本的参数分析及应用，如语音的分割，预处理等。这种分析方法的特点是：①表示语音信号比较直观、物理意义明确。②实现其起来比较简单、预算量少。③可以得到语音的一些重要的参数。④只使用示波器等通用设备，使用较为简单等。
　语音信号的时域参数有短时能量、短时过零率、短时自相关函数等，这是语音信号的一组最基本的短时参数，在各种语音信号数字处理技术中都有应用。

短时能量分析：
　设语音波形时域信号为x(l),分帧加窗处理后得到的第n帧语音信号为 ，则满足下式：
　　　　　　　　
其中，n=0,1T,2T,...,并且N为帧长，T为帧移长度。
　 设第n帧语音信号的短时能量用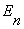表示，则其计算公式如下：

　　　　　　　　　　　　　　　　
是一个度量语音信号幅度值变化的函数。

短时过零率分析：
　短时过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。过零分析是语音时域分析中最简单的一种。对于连续语音信号，过零即以为着时域波形通过时间轴；而对于离散信号，如果相邻的取样值改变符号则成为过零。过零率就是样本改变符号的次数。
定义语音信号的短时过零率为：
　　　　　　　　
式中，sgn[]是符号函数，即：

短时自相关函数：
　相关分析是一种常用的时域波形分析方法，对于确定性离散信号[x(n)]，能量有限，其子相关函数定义为： 　　　(2.1.1)
　如果{x(n)}是随即或者周期性的离散信号，不是能量有限的，那么其自相关函数的定义为：
　由自相关函数的定义可以看出其所具有的一些性质：(1)自相关函数是偶函数，满足R(k)=R(-k); (2)k=0时函数取得最大值，此时，对于确定性信号，自相关函数的取值就是该信号的能量，对于随即信号或者周期信号，自相关函数的取值是该信号的平均功率；(3)如果原序列是周期为T的周期信号，那么自相关函数也是周期为T的周期函数，即R(k)=R(T+k)。
　短时自相关函数的定义为：
上式的物理意义为：首先用窗函数选择要处理的语音，然后将窗选结果带入(2.1)式得到上式。利用自相关函数是偶函数的性质，有
　　　　　
如果定义，上式变形为：
　　　　
即为序列[x(n)x(n-k)]通过单位冲激响应为 的滤波器后的输出。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　back to top

---

频域分析

　语音信号的频域分析就是分析语音信号的频域特征。从广义上讲，语音信号的频域分析包括语音信号的频谱，功率谱，倒频谱等，这里实现了语音信号的线性预测法。线性预测是一种很重要的技术，几乎普遍地应用与语音信号处理的各个方面。
　线性预测分析的基本思想是：由于语音样点之间存在相关性，所以可以用过去的样点值来预测现在或未来的样点值，即一个语音的抽样能够用过去若干个语音抽样或它们的线性组合来逼近。通过使实际语音抽样和线性预测抽样之间的误差在某个准则下达到最小值来决定唯一的一组预测系数。而这组预测系数就反映了语音信号的特征，可以作为语音信号特征参数用与语音识别、语音合成等。
　将线性预测应用与语音信号处理，不仅是因为它的预测功能，而且更重要的是因为它能提供一个非常好的声道模型及模型参数估计方法。线性预测的基本原理和语音信号数字模型密切相关。

　用线性预测误差滤波器来实现，线性预测误差滤波器的传递函数为：
　　　　　 　　　　　　　
其中p为预测器阶数， 为线性预测器系数。
线性预测模型为：
，其中，称为s(n)的预测值。线性预测分析(LPA)实质上就是设计一个预测误差滤波器A(z),即求解使得预测误差e(n)在某个预定的准则下最小。理论上通常采用均方误差最小准则。根据e(n)的定义，的数学期望为：
　　 　　　　　　　
令 ，即
将e(n)代入得
其中是s(n)的自相关序列。
公式　　 可写成(Yule-Walker方程)：r-RA=0
r：自相关矢量
R：自相关矩阵
A：预测系数矢量
自相关矢量、自相关矩阵和预测系数矢量的矩阵表示为：
　　 　　

协方差法：
　协方差法的定义为，其中s(n)的长度范围为：。s(n)的协方差定义为：。
由可得，
即：
　由上面可以看出协方差的特点有：
①不需要加窗，计算精度高
②不满足，即不能保证系统的稳定性，进行线性预测分析时，不得不随时判定H(z)的极点位置，不断加以修正，才能得到稳定的结果

伯格法：
　伯格法的基本思想是使正向和反向预测误差的平方和最小，即
。　　令，则
，由Schwarz不等式可以证明：。
Burg法能保证合成滤波器的稳定。

RMLE：
　 这里将要描述另一种估计模型参数的方法。RMLE(recursive maximum likelihood estimator)，是一种接近于MLE但是采用线性预测的方法，它采用的是递归的方式。

感知线性预测法：
感知线性预测(PLP)分析法基于许多听觉的心理学概念。它的整个流程块图如下：
　 　　　　　　　
语谱分析：

　最常用的语谱分析是periodogram,它的定义如下：
　　　 　　　　
其中X(n)是一个任意的序列．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　back to top

---

倒谱分析

　语音信号的倒谱分析就是求取语音倒谱特征参数的过程，它可以通过同态处理来实现。同态信号处理也成为同态滤波，它实现了将卷积关系变换为求和关系的分离处理，即解卷。对语音信号进行解卷，可将语音信号的声门激励信息及声道响应信息分离开来，从而求得声道共振特性和基音周期，用与语音编码、合成、识别等。对语音信号进行解卷，求取倒谱特征参数的方法有两种：一是线性预测分析，一是同态分析处理。这里我们讨论通过同态处理的倒谱分析方法。

　如图2.3a所示为一卷积同态系统的模型，该系统的输入卷积信号经过系统变换后输出的是一个处理过的卷积信号。这种同态系统可分解为三个子系统，如图2.3b所示，即两个特征子系统和一个线性子系统。第一个子系统(如图2.3c)，它完成将卷积性信号转化为加性信号的运算；第二个子系统是一个普通线性系统，满足线性叠加原理，用于对加性信号进行线性变换；第三个子系统是第一个子系统的逆变换，它将加性信号反变换为卷积信号，如图2.3d所示。在图2.3中，符号*、+和.分别表示卷积、加法和乘法。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　back to top

---

WRLS-VFF分析

若要做WRLS-VFF分析，首先我们要先引进一个假设：所有的语音信号都是用以下的模型产生的。

　　　　　　　　

并引入两个定义，一个为参数矢量，一个为数据矢量。如下等式所示：

通过以上所引入的一个假设，两个定义，我们可以定义一个完整且稳定的带输入估计的WRLS-VFF算法，其核心定义如下：
Prediction error:

Gain update:

Forgetting factor:

Input estimate:
a)if λk<λ0 then
　　　　
b)if λk>λ0 then
　　　　
Parameter update:

Covariance matrix:

　　　　　　　　　　　　　　　　　　　　　　　　　　　　back to top